Bhen and Geri run an ice cream business in the town of Palouse, WA. To produce the ice cream, they hire labor L at a wage of W dollars per worker. L is the only input in production. L workers produce Y pints of ice cream according to the production function, Y = F(L) = 10L − ( 1 2 )L 2 . They then sell the ice cream at the price of P dollars per pint of ice cream. 1. Plot the production function in a graph (with L on the X-axis and Y on the Y-axis) for values of labor L = 0, …, 10. 2. Write the firm’s profit function in terms of labor, Π(L). Then plot the firm’s profits for values of labor L = 0, …, 10 for price P = 2 and wage W = 4. From your graph, at what value of L do profits appear to be maximized? 3. The MPL function (∆Y/∆L) for the production function given above is: MPL(L) = 10 − L. Plot the MPL function for values of labor L = 0, …, 10. How does the MPL change with the level of L employed? In this example, are there diminishing returns to labor? 4. State the condition on labor demand for which profits are maximized. 5. For the wage W = 4 and price P = 2, what is the profit maximizing level of labor demand, L ∗ ? 6. Given the same price and wage as in Part 5, how many pints of ice cream do Bhen and Geri produce under profit maximization (Y ∗ )? What are their profits? 7. Now suppose Ferdinand’s starts selling ice cream in Palouse, which drives down the price that Bhen and Geri can get for a pint of their ice cream to P = 1. What is the new profit maximizing level of labor demand (L ∗ )? Now how many pints are produced (Y ∗ )? Now what are profits? 8. Is Bhen and Geri’s supply curve upward sloping between P = 1 and P = 2 (remember that a supply curve is the relationship between price P and optimal output Y ∗ )?
Essay Writing Service Features
Our Experience
No matter how complex your assignment is, we can find the right professional for your specific task. Writing Errands is an essay writing company that hires only the smartest minds to help you with your projects. Our expertise allows us to provide students with high-quality academic writing, editing & proofreading services.
Free Features
Free revision policy
$10Free bibliography & reference
$8Free title page
$8Free formatting
$8How Our Essay Writing Service Works
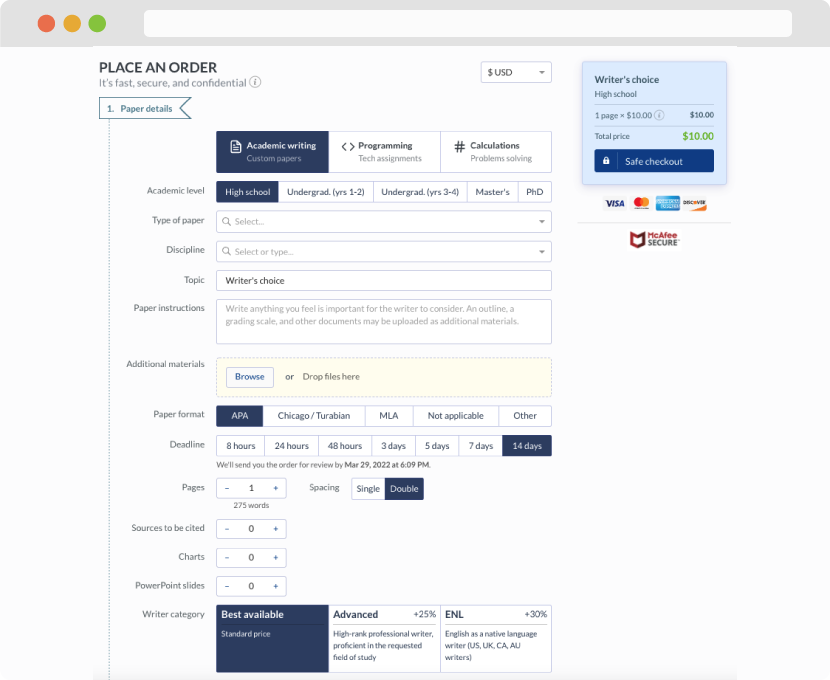
First, you will need to complete an order form. It's not difficult but, in case there is anything you find not to be clear, you may always call us so that we can guide you through it. On the order form, you will need to include some basic information concerning your order: subject, topic, number of pages, etc. We also encourage our clients to upload any relevant information or sources that will help.
Complete the order form
Once we have all the information and instructions that we need, we select the most suitable writer for your assignment. While everything seems to be clear, the writer, who has complete knowledge of the subject, may need clarification from you. It is at that point that you would receive a call or email from us.
Writer’s assignment
As soon as the writer has finished, it will be delivered both to the website and to your email address so that you will not miss it. If your deadline is close at hand, we will place a call to you to make sure that you receive the paper on time.
Completing the order and download